

Simulation packages developed at the
Marian group
1. Lattice Kinetic Monte Carlo (LKMC) Simulator (with Chen-Hsi Huang)
 <
Download (github) >
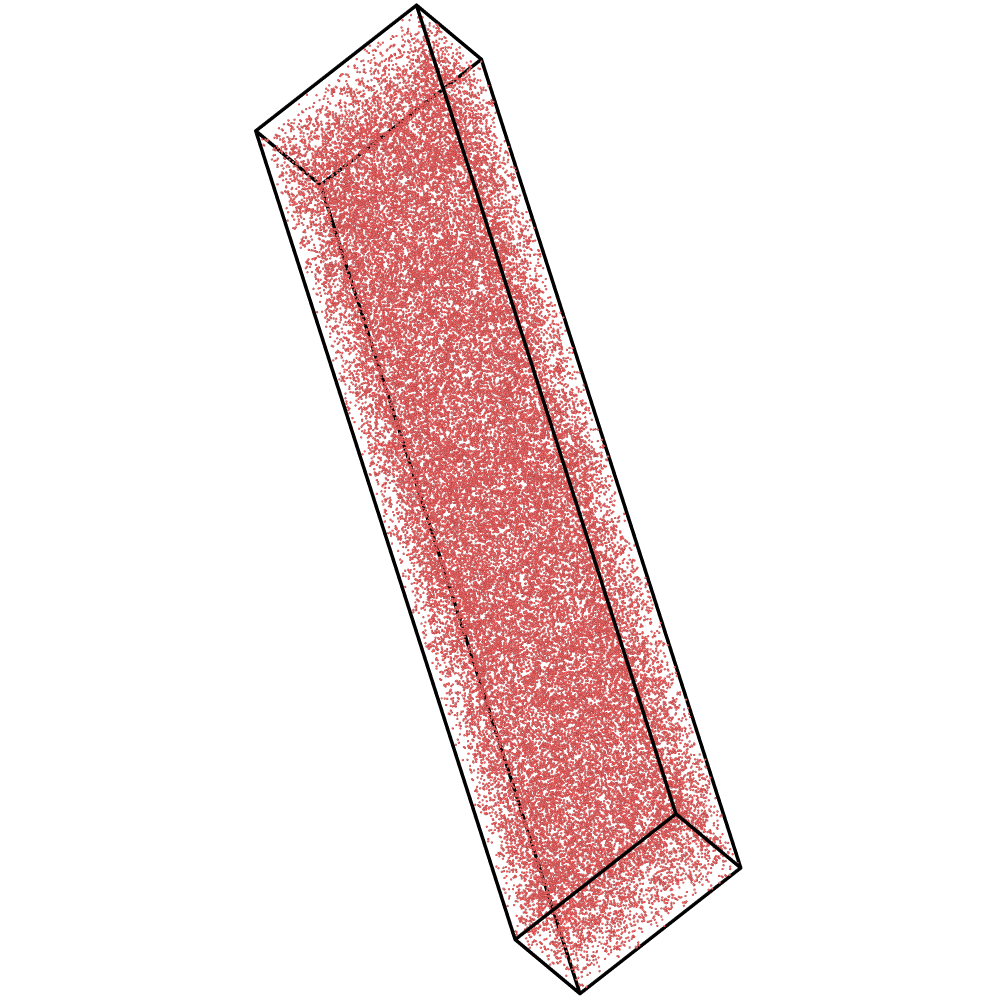
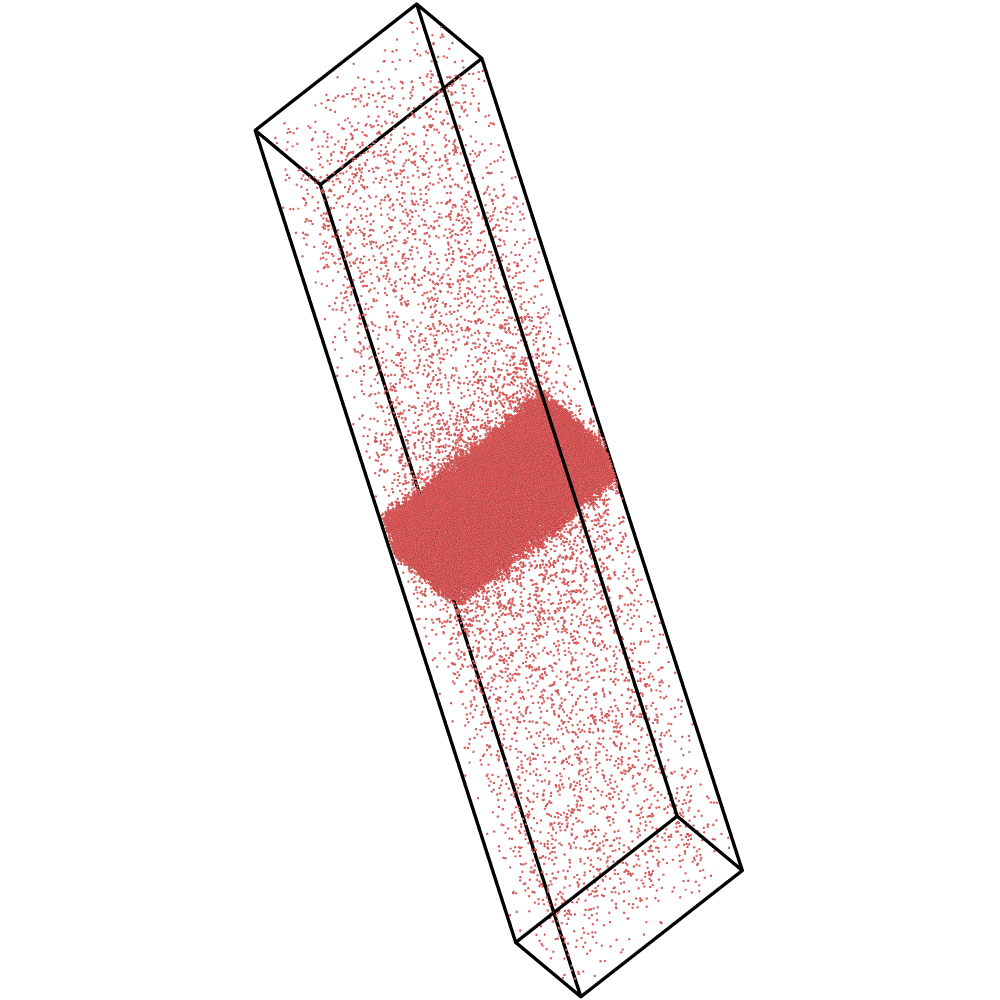
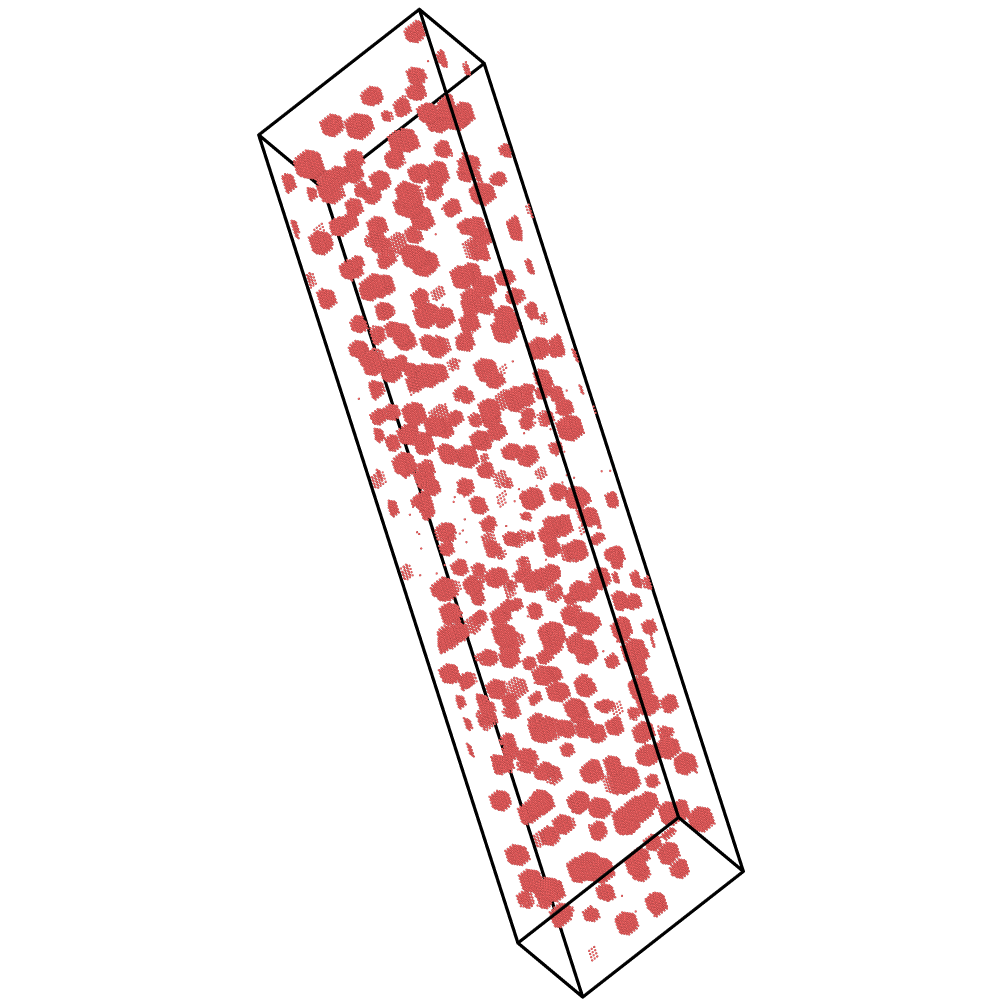
The LKMC simulation package can be used to study microstructural evolution of metal alloys
under various scenarios, including annealing and irradiation. The code uses a primitive lattice reconstruction to construct FCC, BCC, and HCP rigid crystal lattices. Diffusion is
simulated by way defect-mediated atomic transport. The LKMC simulation package includes
transport by both vacancy and interstitials. We have used it to study alloy evolution in
Fe-Cu, Ni-Au, and W-Re. The code is written in C++.
To know more about the details of the code please see the README.md file.
<
Download (github) >
The LKMC simulation package can be used to study microstructural evolution of metal alloys
under various scenarios, including annealing and irradiation. The code uses a primitive lattice reconstruction to construct FCC, BCC, and HCP rigid crystal lattices. Diffusion is
simulated by way defect-mediated atomic transport. The LKMC simulation package includes
transport by both vacancy and interstitials. We have used it to study alloy evolution in
Fe-Cu, Ni-Au, and W-Re. The code is written in C++.
To know more about the details of the code please see the README.md file.
2. Stochastic Cluster Dynamics (SCD) Simulator (with Chen-Hsi Huang)
 <
Download (github) >
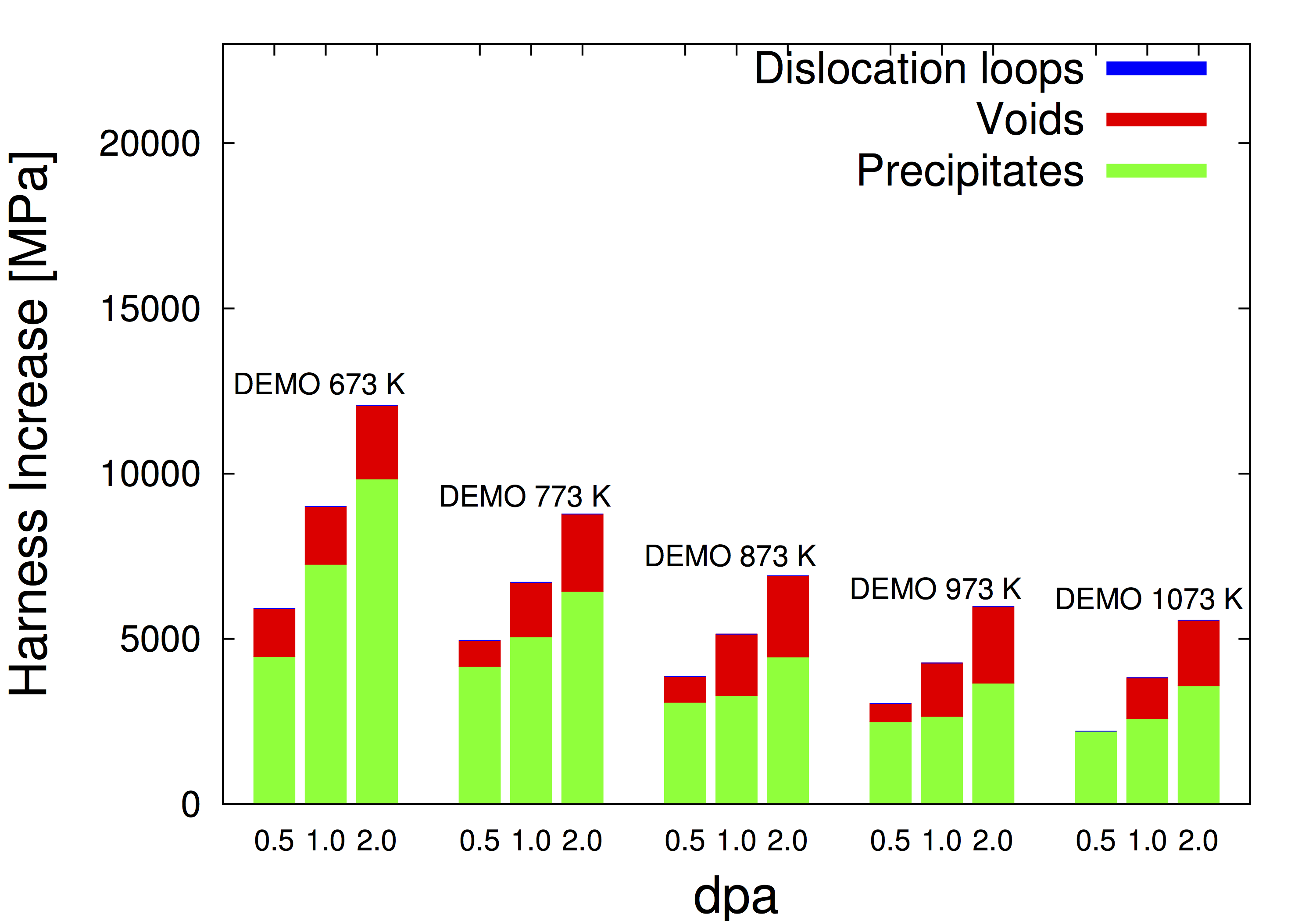
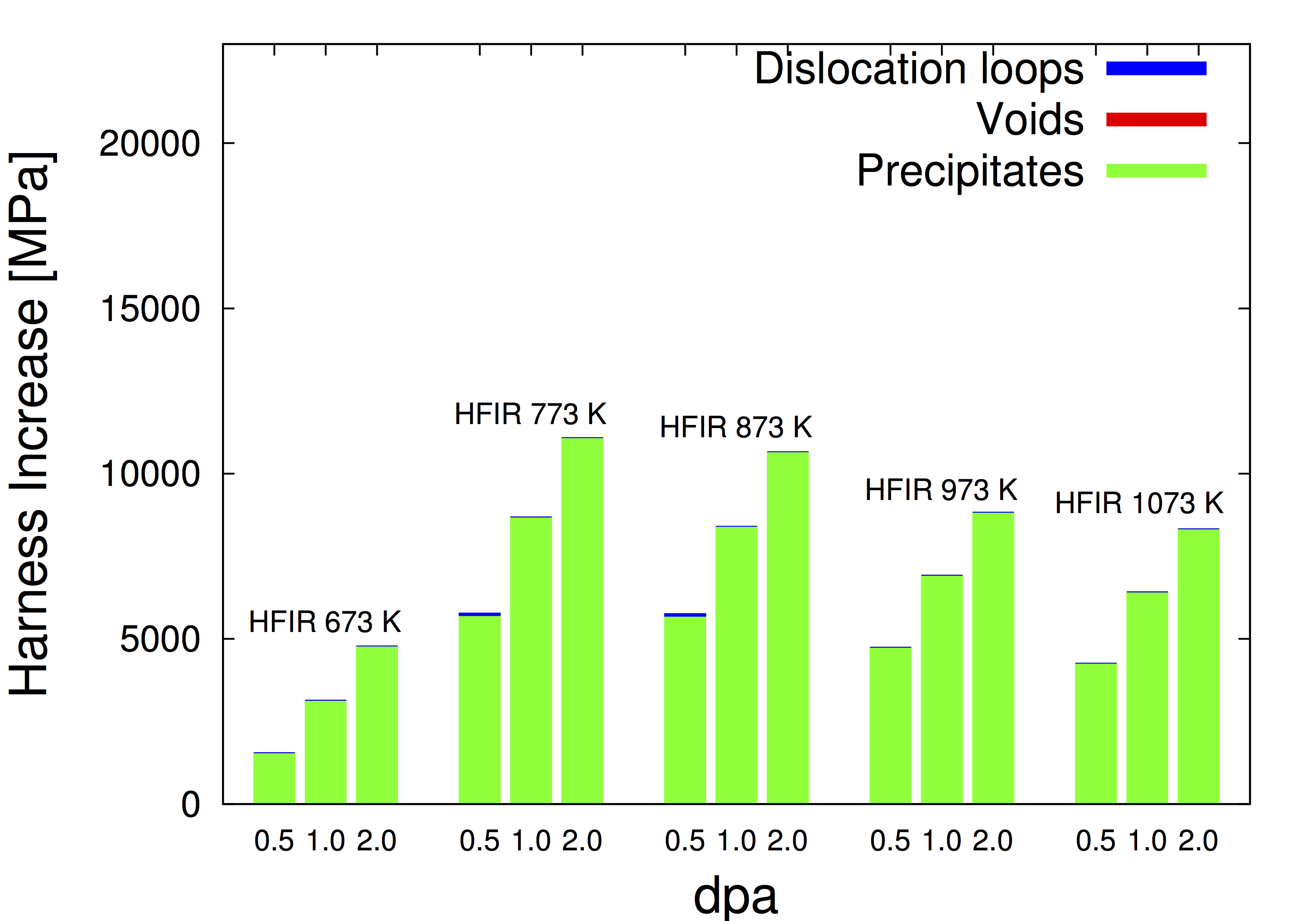
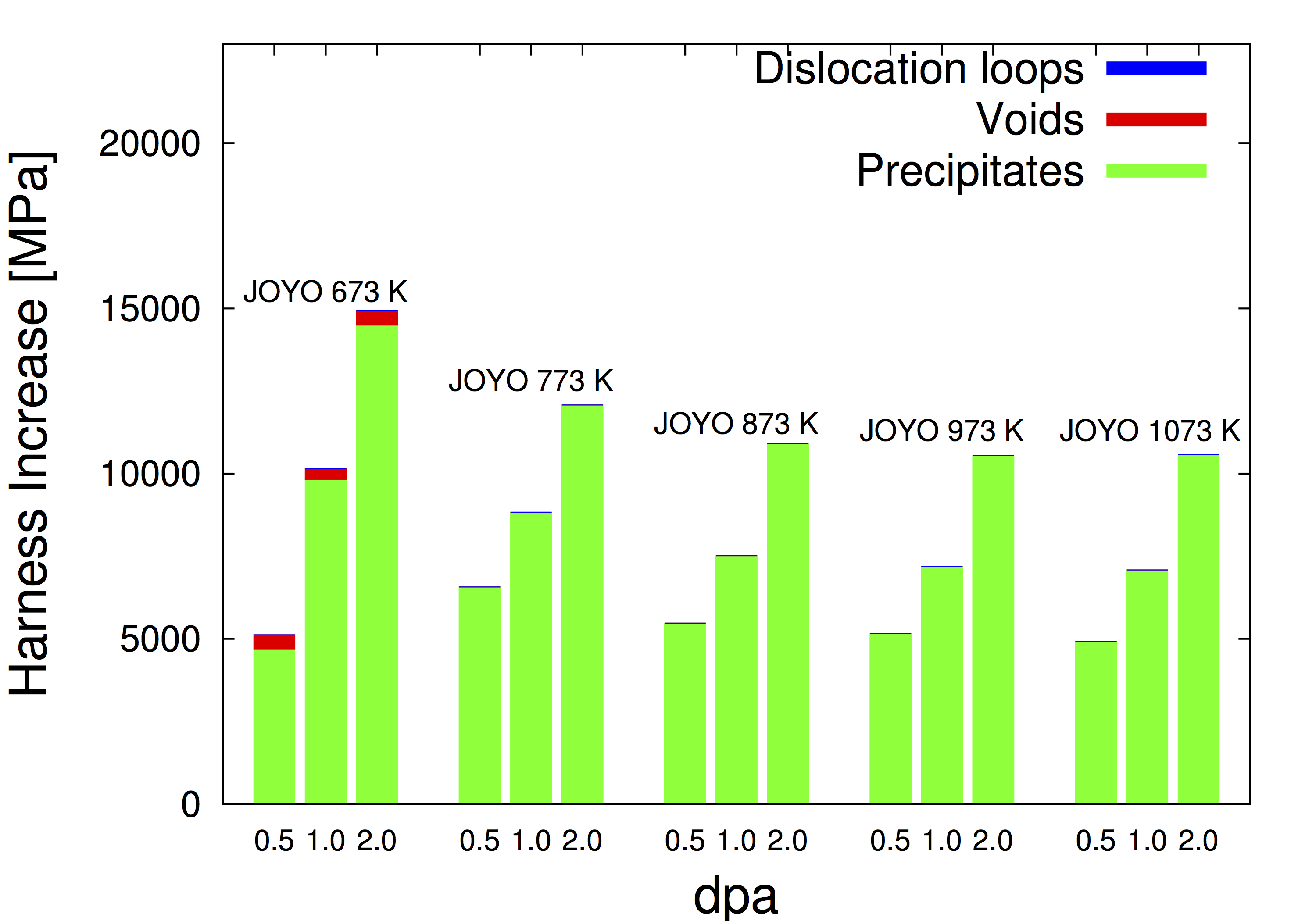
The SCD simulation package contains a computer code written in C used to study the evolution
of defect and solute clusters under the mean-field approximation using a stochastic solver.
The code can be used to study multispecies condtions such as under fusion irradiation including transmutation. The present parameterization is for the W-Re alloy but we have used the code for
W-He, Fe-Cr, and Fe-He-H.
<
Download (github) >
The SCD simulation package contains a computer code written in C used to study the evolution
of defect and solute clusters under the mean-field approximation using a stochastic solver.
The code can be used to study multispecies condtions such as under fusion irradiation including transmutation. The present parameterization is for the W-Re alloy but we have used the code for
W-He, Fe-Cr, and Fe-He-H.
3. A two-dimensional implementation of a diffuse interface polycrystal plasticity model with grain boundary evolution (with Nikhil Admal)
 <
Download (github) >
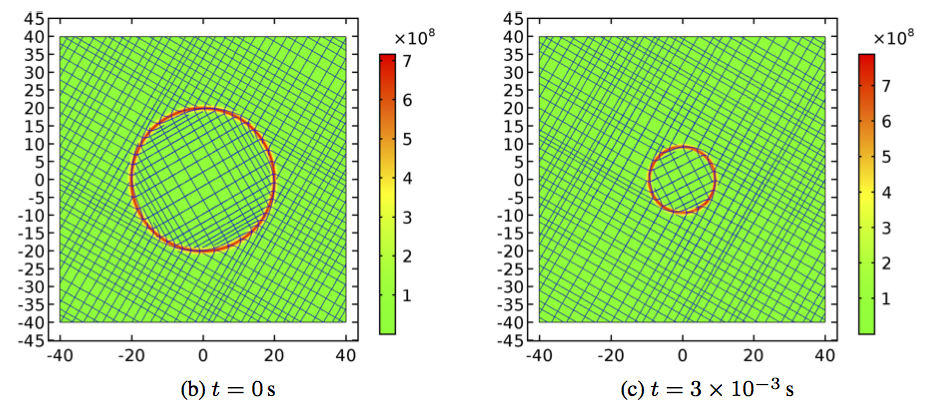
This package contains a 2D COMSOL implementation of a diffuse-interface polycrystal plasticity
model with grain boundary evolution demonstrating coupled grain boundary motion, grain rotation and sliding, and dynamic recovery as described in our paper .
<
Download (github) >
This package contains a 2D COMSOL implementation of a diffuse-interface polycrystal plasticity
model with grain boundary evolution demonstrating coupled grain boundary motion, grain rotation and sliding, and dynamic recovery as described in our paper .
4. MS-STEM-FEM package for multi-slice scanning transmission electron microscopy simulations (with Nick Julian)
 <
Download (github) >
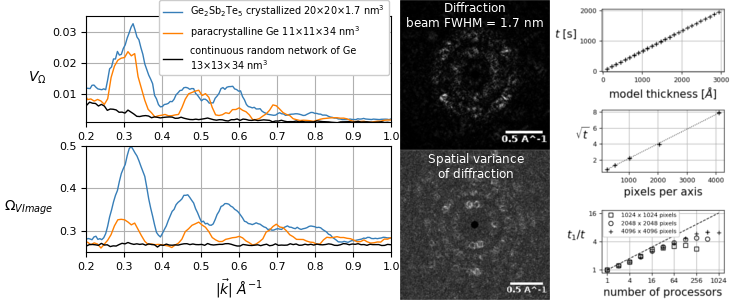
MS-STEM-FEM is a multi-slice scanning transmission electron microscopy
(STEM) simulation tool with integrated routines to simulate
fluctuation electron microscopy (FEM) experiments as they are
performed in a STEM mode microscope. The FEM measurement provides a
method of distinguishing between completely disordered and partially
ordered materials, but is sensitive to material thickness as explored
in our paper . Written in C++ and parallelized with MPI, MS-STEM-FEM scales
linearly with model thickness, enabling STEM-FEM simulations using
models of the same thicknesses as measured experimentally and an
improved ability to relate atomic models and experimental measurements
of glassy materials.
<
Download (github) >
MS-STEM-FEM is a multi-slice scanning transmission electron microscopy
(STEM) simulation tool with integrated routines to simulate
fluctuation electron microscopy (FEM) experiments as they are
performed in a STEM mode microscope. The FEM measurement provides a
method of distinguishing between completely disordered and partially
ordered materials, but is sensitive to material thickness as explored
in our paper . Written in C++ and parallelized with MPI, MS-STEM-FEM scales
linearly with model thickness, enabling STEM-FEM simulations using
models of the same thicknesses as measured experimentally and an
improved ability to relate atomic models and experimental measurements
of glassy materials.
5. Three dimensional kinetic Monte Carlo code for screw dislocation-solute interactions in W-Re and W-O (with Yue Zhao)
 <
Download (github) >
Screw dislocation motion in body-centered cubic (bcc) metals is a thermally activated process controlled by kink-pair nucleation. Similarly, solute diffusion in a bcc lattice is generally also thermally activated, consisting of first-nearerst neighbor lattice jumps. To properly investigate dislocation-solute interactions, one has to treat both processes within the same framework. The best such framework is kinetic Monte Carlo (kMC), where events are sampled with the correct probability and time is advanced using an exponential distribution. As described in our paper, these interactions can result in hardening, softening, or both, depending on temperature and solid concentration. The figure above shows the strain rate-temperature map where dynamic strain ageing is observed in W-O, i.e. dislocaion-solute coevolution. The red region delimits the space where solutes and dislocations evolve on similar time scales. The dashed lines in the figure represent thermally activated transitions into the DSA region, each with its own activation energy. The code package is written in C++ and based on the first version of the KMC by Alexander Stukowski (which can also be released upon request).
<
Download (github) >
Screw dislocation motion in body-centered cubic (bcc) metals is a thermally activated process controlled by kink-pair nucleation. Similarly, solute diffusion in a bcc lattice is generally also thermally activated, consisting of first-nearerst neighbor lattice jumps. To properly investigate dislocation-solute interactions, one has to treat both processes within the same framework. The best such framework is kinetic Monte Carlo (kMC), where events are sampled with the correct probability and time is advanced using an exponential distribution. As described in our paper, these interactions can result in hardening, softening, or both, depending on temperature and solid concentration. The figure above shows the strain rate-temperature map where dynamic strain ageing is observed in W-O, i.e. dislocaion-solute coevolution. The red region delimits the space where solutes and dislocations evolve on similar time scales. The dashed lines in the figure represent thermally activated transitions into the DSA region, each with its own activation energy. The code package is written in C++ and based on the first version of the KMC by Alexander Stukowski (which can also be released upon request).
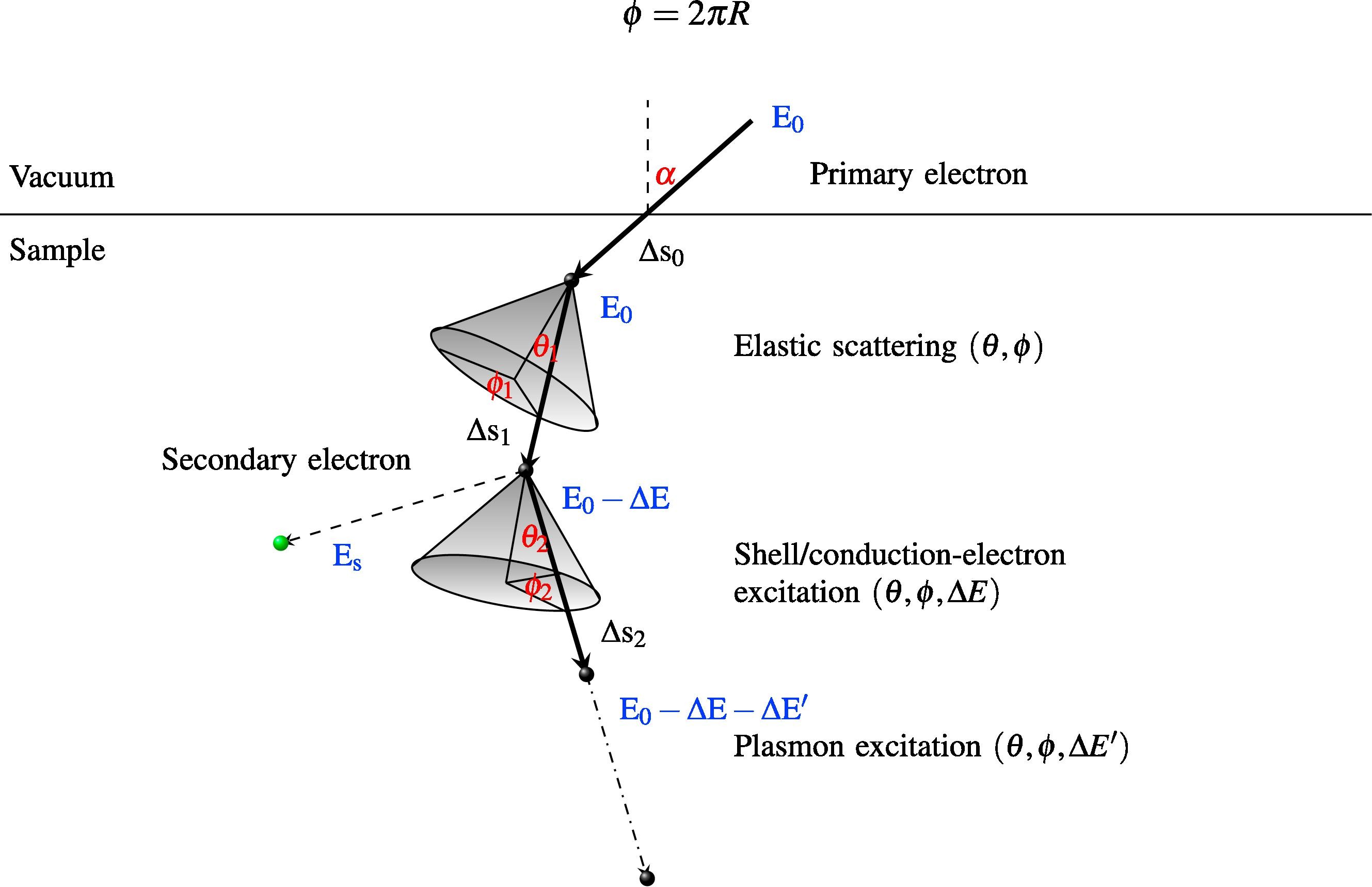
6a. Three dimensional scattering Monte Carlo code for calculations of secondary electron emission from flat surfaces (with Iris Chang)
 <
Download (github) >
When a material is bombarded with electrons, a series of scattering processes take place inside it through collisions with ions and other electrons. Through these collisions, electrons already existing in the material receive sufficient energy from the incoming electrons to become activated, leaving their initial positions and initiationg their own internal scattering trajectories. As described in this paper, a fraction of those 'secondary' electrons makes it back to the surface of the material, resulting in a net nonzero emission rate. The package linked here contains Python files to simulate electron scattering processes both in metallic and ceramic materials.
<
Download (github) >
When a material is bombarded with electrons, a series of scattering processes take place inside it through collisions with ions and other electrons. Through these collisions, electrons already existing in the material receive sufficient energy from the incoming electrons to become activated, leaving their initial positions and initiationg their own internal scattering trajectories. As described in this paper, a fraction of those 'secondary' electrons makes it back to the surface of the material, resulting in a net nonzero emission rate. The package linked here contains Python files to simulate electron scattering processes both in metallic and ceramic materials.
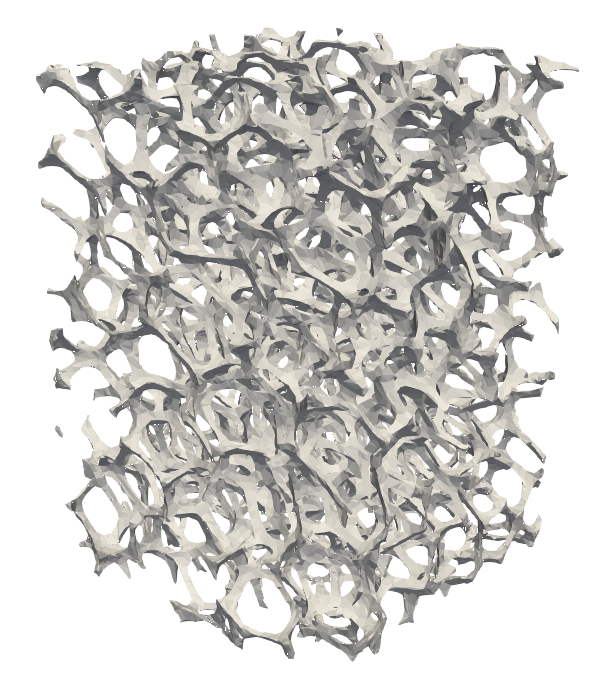
6b. Three dimensional raytracing Monte Carlo code for calculations of secondary electron emission and sputtering in complex geometries (with Andrew Alvarado and Iris Chang)
 <
Download (github) >
The code package in item 6a above is for flat (ideal) surfaces. However, real material surfaces are never perfectly flat. Moreover, particle irradiation can result over time in significant morpohological changes that create roughness and structure. Hence, methods that can capture surface evolution as surfaces are irradiated are needed for morphology predictions. As described in our paper, raytracing Monte Carlo coupled to surface mesh evolution provides an ideal platform to study irradiation of arbitrary surface geometries, such as the microfoam structure shown in the figure. The package linked here contains a raytracing module that simulates single particle ray interactions with discrete surface elements of a given mesh. These interactions are determined according to the phsyics of electron--matter or ion-matter interactions (as described in 6a), which are characterized using scattering Monte Carlo simulations. Lastly, a mesh evolution module gives the time behavior of the structure if and when appropriate.
<
Download (github) >
The code package in item 6a above is for flat (ideal) surfaces. However, real material surfaces are never perfectly flat. Moreover, particle irradiation can result over time in significant morpohological changes that create roughness and structure. Hence, methods that can capture surface evolution as surfaces are irradiated are needed for morphology predictions. As described in our paper, raytracing Monte Carlo coupled to surface mesh evolution provides an ideal platform to study irradiation of arbitrary surface geometries, such as the microfoam structure shown in the figure. The package linked here contains a raytracing module that simulates single particle ray interactions with discrete surface elements of a given mesh. These interactions are determined according to the phsyics of electron--matter or ion-matter interactions (as described in 6a), which are characterized using scattering Monte Carlo simulations. Lastly, a mesh evolution module gives the time behavior of the structure if and when appropriate.
7. Stochastically-driven field evolution in multi-phase materials (with Nick Julian)
 <
Download (github) >
SPF (stochastic phase field) is a collection of functions and
executables written to demonstrate stochastically driven field
evolution using a fixed time increment and a rectangular grid, driven
by either continuous-in-time Gaussian noise or discrete Poisson noise
representative of either Brownian motion or a jump process,
respectively. Special care is given to the methods required to
accurately integrate the stochastic differential equations.
Specifically, SPF contains an implementation of the Marcus canonical
integral applicable to Levy processes. SPF is parallelized by MPI and
released under GPLv2. Work done in collaboration with
Prof. Enrique Martinez .
<
Download (github) >
SPF (stochastic phase field) is a collection of functions and
executables written to demonstrate stochastically driven field
evolution using a fixed time increment and a rectangular grid, driven
by either continuous-in-time Gaussian noise or discrete Poisson noise
representative of either Brownian motion or a jump process,
respectively. Special care is given to the methods required to
accurately integrate the stochastic differential equations.
Specifically, SPF contains an implementation of the Marcus canonical
integral applicable to Levy processes. SPF is parallelized by MPI and
released under GPLv2. Work done in collaboration with
Prof. Enrique Martinez .
8. Spatially-resolved stochastic cluster dynamics code package (with Qianran Yu)
 <
Download (github) >
Package 2 above includes a version of the SCD code that assumes uniform conditions in a 3D volume under th emean-field approximation. However, in many instances one has to to deal with finite geometries at least along one spatial dimension. As described in our paper, this directionality involves solving a generalized diffusion equation that captures defect transport into and out of a representative volume element. Thus this package is suited for irradiation conditions where the source of defects is not volumetrically uniform, such as in the case of ion implantation on a thin film, or penetration of light ions by epithermal exposure on heavy metal surfaces, such as He or H deposition on W surfaces in divertor thermal shield materials. One of the findings of the paper referenced above is that hydrogen bubbles in pre-irradiated form with various internal pressures depending on penetration depth, as schematically shown in the following figure.
<
Download (github) >
Package 2 above includes a version of the SCD code that assumes uniform conditions in a 3D volume under th emean-field approximation. However, in many instances one has to to deal with finite geometries at least along one spatial dimension. As described in our paper, this directionality involves solving a generalized diffusion equation that captures defect transport into and out of a representative volume element. Thus this package is suited for irradiation conditions where the source of defects is not volumetrically uniform, such as in the case of ion implantation on a thin film, or penetration of light ions by epithermal exposure on heavy metal surfaces, such as He or H deposition on W surfaces in divertor thermal shield materials. One of the findings of the paper referenced above is that hydrogen bubbles in pre-irradiated form with various internal pressures depending on penetration depth, as schematically shown in the following figure.

9. Stochastic solver based on the residence-time algorithm for crystal plasticity (with Qianran Yu)
 <
Download (github) >
The deformation of crystalline materials by dislocation motion takes place in discrete amounts determined by the Burgers vector. Dislocations may move individually or in bundles, potentially giving rise to intermittent slip. This confers plastic deformation with a certain degree of variability that can be interpreted as being caused by stochastic fluctuations in dislocation behavior. However, crystal plasticity (CP) models are almost always formulated in a deterministic sense, assuming that fluctuations average out over large material volumes and/or cancel out due to multi-slip contributions. Here, a stochastic solver for CP models based on the residence-time algorithm (as explained in our paper) is provided. The solver naturally captures plastic fluctuations by sampling among the set of active slip systems in the crystal, solving the evolution equations of explicit CP formulations, which are recast as stochastic ordinary differential equations and integrated discretely in time. The stochastic CP model is numerically stable by design and naturally breaks the symmetry of plastic slip by sampling among the active plastic shear rates with the correct probability. This can lead to phenomena such as intermittent slip or plastic localization without adding external symmetry-breaking operations to the model.
<
Download (github) >
The deformation of crystalline materials by dislocation motion takes place in discrete amounts determined by the Burgers vector. Dislocations may move individually or in bundles, potentially giving rise to intermittent slip. This confers plastic deformation with a certain degree of variability that can be interpreted as being caused by stochastic fluctuations in dislocation behavior. However, crystal plasticity (CP) models are almost always formulated in a deterministic sense, assuming that fluctuations average out over large material volumes and/or cancel out due to multi-slip contributions. Here, a stochastic solver for CP models based on the residence-time algorithm (as explained in our paper) is provided. The solver naturally captures plastic fluctuations by sampling among the set of active slip systems in the crystal, solving the evolution equations of explicit CP formulations, which are recast as stochastic ordinary differential equations and integrated discretely in time. The stochastic CP model is numerically stable by design and naturally breaks the symmetry of plastic slip by sampling among the active plastic shear rates with the correct probability. This can lead to phenomena such as intermittent slip or plastic localization without adding external symmetry-breaking operations to the model.

10. Coupled polycrystal plasticity/vertex dynamics model for polycrystal deformation and recrystallization (with Cameron McElfresh)
<
Download (github) >
Recrystallization of deformed polycrystalline metallic alloys is a fundamental process in metallurgy,
where the material achieves a more ductile state after deofrmation by cold-working.
As such, models designed to study recrystallization must capture both deformation and grain boundary evolution,
ideally simultaneously. This package contains routines that create COMSOL-compatible scripts of prolycrystalline
metals, and a discrete vertex dynamics model that evolves the grain boundary structure in response
to curvature and plastic strain energy driving forces.

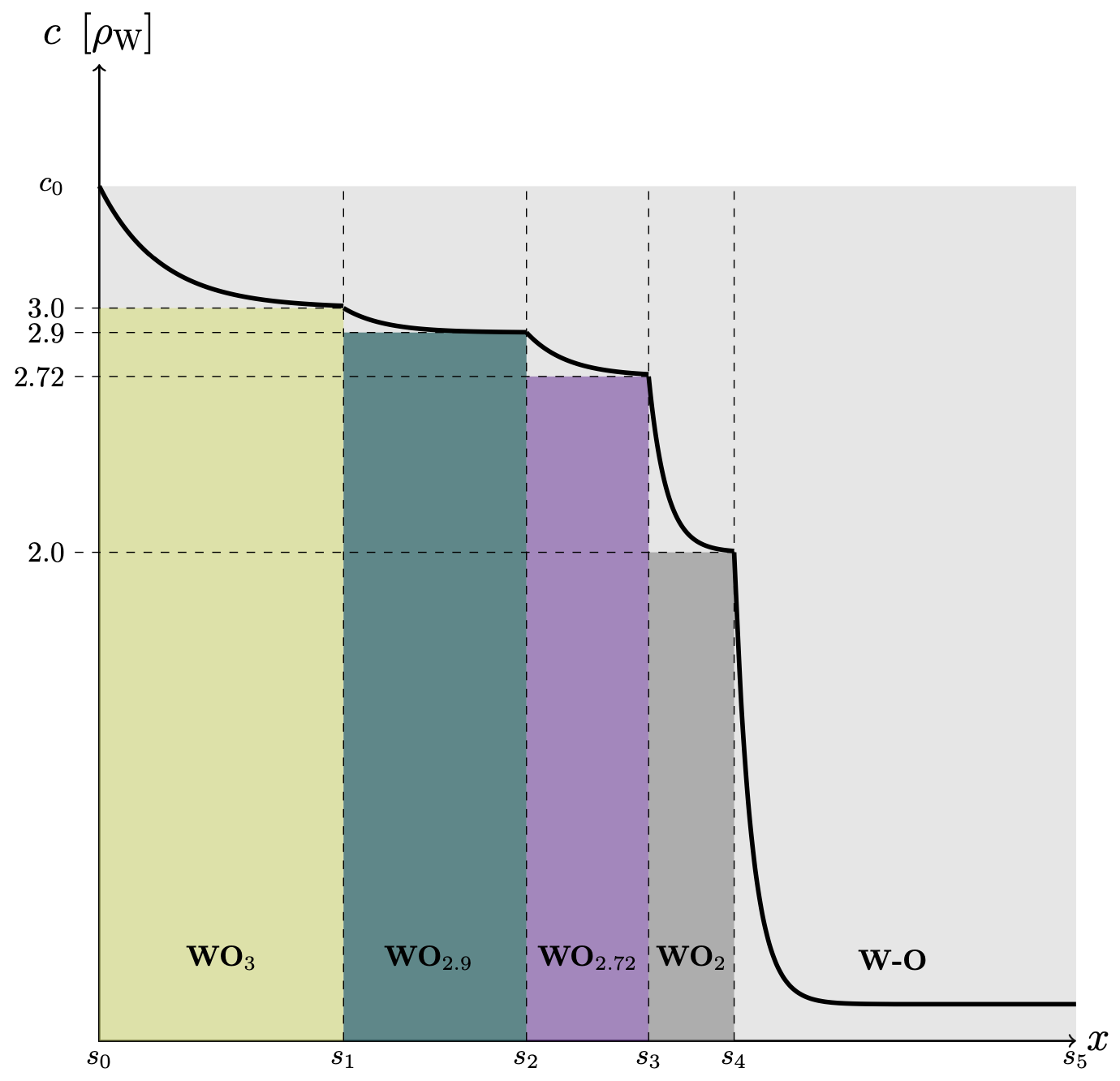
11. Multilayer interface tracking method for studying tungsten oxidation kinetics (with Shu Huang)
<
Download (github) >
This package contains a numerical model to predict oxide scale growth on tungsten surfaces under exposure to oxygen at high temperatures. The model captures the formation of four thermodynamically-compatible oxide sublayers, WO2, WO2.72, WO2.9, and WO3, on top of the metal substrate. Oxide layer growth is simulated by tracking the oxide/oxide and oxide/metal interfaces using a sharp-interface Stefan model coupled to diffusion kinetics. The model is parameterized using selected experimental measurements and electronic structure calculations of the diffusivities of all the oxide subphases involved. We simulate oxide growth at temperatures of 600C and above, extracting the power law growth exponents in each case, which we find to deviate from classical parabolic growth in several cases. We conduct a comparison of the model predictions with an extensive experimental data set, with reasonable agreement at most temperatures. While many gaps in our understanding still exist, this work is a first attempt at embedding the thermodynamic and kinetic complexity of tungsten oxide growth into a comprehensive mesoscale kinetic model that attempts to capture the essential features of tungsten oxidation to fill existing knowledge gaps and guide and enhance future tungsten oxidation models.
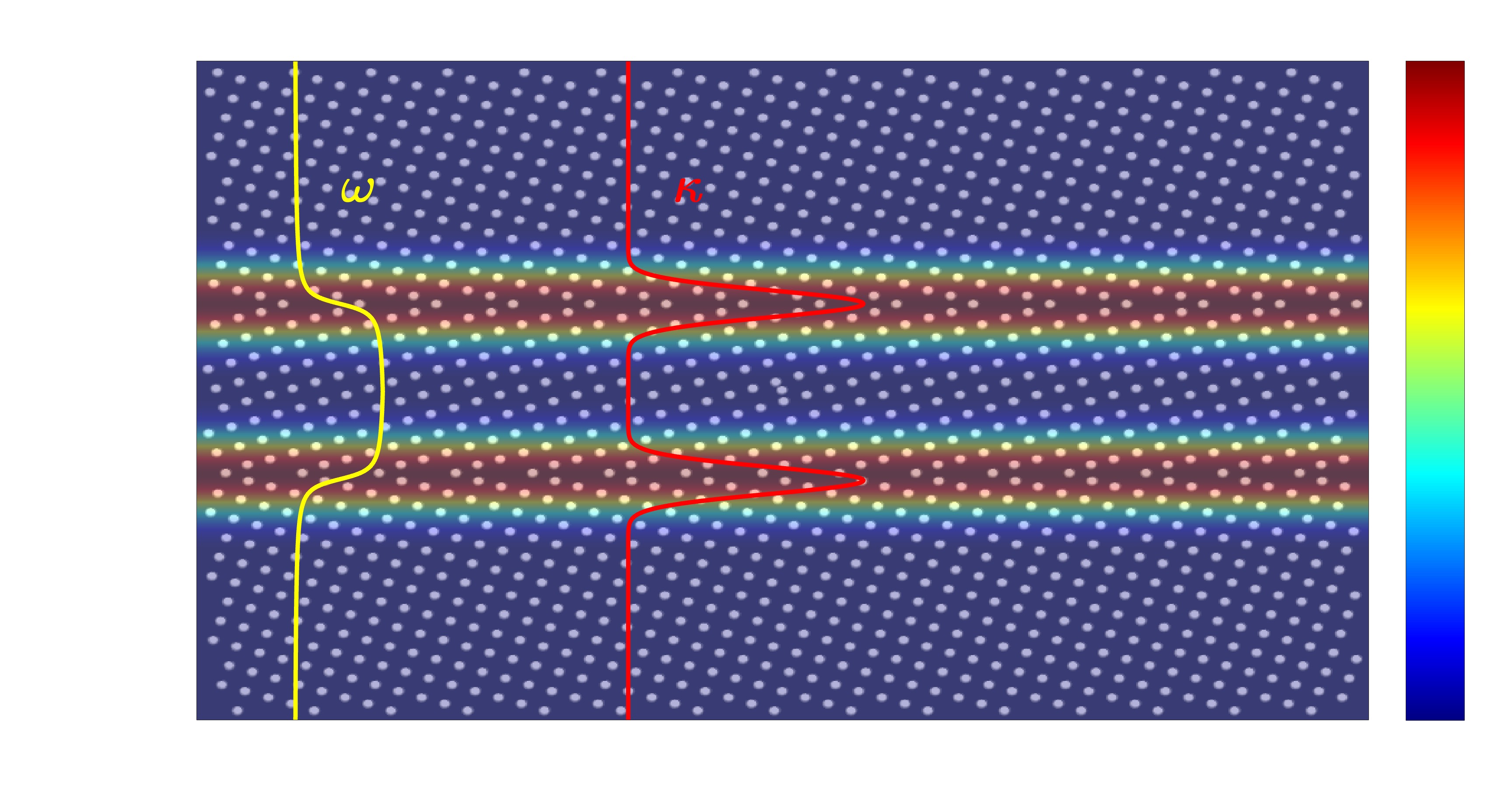
12. Code for generating geometrically-necessary dislocation fingerprints of prismatic loop networks (with Sicong He)
<
Download (github) >
Geometrically-necessary dislocations (GND) are dislocations that accommodate lattice curvature due to
nonuniform plastic deformation. These dislocation have net nonzero Burgers vector and do not contribute to plastic
strain per se. As a consequence, GND are a measure of plastic distortion and can thus provide useful information
on lattice rotation associated with slip, grain boundary motion, or plastic strain gradients. Strictly speaking, GND are
defined by the dislocation density tensor (also known as the GND tensor), which can be obtained as a line integral over all
dislocations within a given volume. However, under some assumptions, the dislocation density tensor can be approximated by
the Nye formula, which relates the GND content withing that volume to the local lattice curvature.
As such, one can use this equivalence to relate the dislocation content to the lattice curvature, or vice versa.
The package included here involves the calculation of spatially resolved GND signals from dislocation configurations obtained
using discrete dislocation dynamics (DDD). To mimic the spatial discretization in precession electron diffraction tests, we
use a three-dimensional tessellation of the DDD supercells. We study GND footprints using both regular structured meshes
(uniform cell size and shape) as well as general Voronoi tessellations with fixed average cell size. The code then performs
cell edge detection by overlaying DDD three-dimensional information on the discretized meshed volume, followed by GND tensor
determination. GND signals are then obtained as the L1 norm of the GND tensor, and final intensities are represented as
smeared versions of discrete signals using a normalized Gaussian spread function.




 <
Download (github) >
The LKMC simulation package can be used to study microstructural evolution of metal alloys
under various scenarios, including annealing and irradiation. The code uses a primitive lattice reconstruction to construct FCC, BCC, and HCP rigid crystal lattices. Diffusion is
simulated by way defect-mediated atomic transport. The LKMC simulation package includes
transport by both vacancy and interstitials. We have used it to study alloy evolution in
Fe-Cu, Ni-Au, and W-Re. The code is written in C++.
To know more about the details of the code please see the README.md file.
<
Download (github) >
The LKMC simulation package can be used to study microstructural evolution of metal alloys
under various scenarios, including annealing and irradiation. The code uses a primitive lattice reconstruction to construct FCC, BCC, and HCP rigid crystal lattices. Diffusion is
simulated by way defect-mediated atomic transport. The LKMC simulation package includes
transport by both vacancy and interstitials. We have used it to study alloy evolution in
Fe-Cu, Ni-Au, and W-Re. The code is written in C++.
To know more about the details of the code please see the README.md file.


 <
Download (github) >
The SCD simulation package contains a computer code written in C used to study the evolution
of defect and solute clusters under the mean-field approximation using a stochastic solver.
The code can be used to study multispecies condtions such as under fusion irradiation including transmutation. The present parameterization is for the W-Re alloy but we have used the code for
W-He, Fe-Cr, and Fe-He-H.
<
Download (github) >
The SCD simulation package contains a computer code written in C used to study the evolution
of defect and solute clusters under the mean-field approximation using a stochastic solver.
The code can be used to study multispecies condtions such as under fusion irradiation including transmutation. The present parameterization is for the W-Re alloy but we have used the code for
W-He, Fe-Cr, and Fe-He-H.
 <
Download (github) >
This package contains a 2D COMSOL implementation of a diffuse-interface polycrystal plasticity
model with grain boundary evolution demonstrating coupled grain boundary motion, grain rotation and sliding, and dynamic recovery as described in our paper .
<
Download (github) >
This package contains a 2D COMSOL implementation of a diffuse-interface polycrystal plasticity
model with grain boundary evolution demonstrating coupled grain boundary motion, grain rotation and sliding, and dynamic recovery as described in our paper .
 <
Download (github) >
MS-STEM-FEM is a multi-slice scanning transmission electron microscopy
(STEM) simulation tool with integrated routines to simulate
fluctuation electron microscopy (FEM) experiments as they are
performed in a STEM mode microscope. The FEM measurement provides a
method of distinguishing between completely disordered and partially
ordered materials, but is sensitive to material thickness as explored
in our paper . Written in C++ and parallelized with MPI, MS-STEM-FEM scales
linearly with model thickness, enabling STEM-FEM simulations using
models of the same thicknesses as measured experimentally and an
improved ability to relate atomic models and experimental measurements
of glassy materials.
<
Download (github) >
MS-STEM-FEM is a multi-slice scanning transmission electron microscopy
(STEM) simulation tool with integrated routines to simulate
fluctuation electron microscopy (FEM) experiments as they are
performed in a STEM mode microscope. The FEM measurement provides a
method of distinguishing between completely disordered and partially
ordered materials, but is sensitive to material thickness as explored
in our paper . Written in C++ and parallelized with MPI, MS-STEM-FEM scales
linearly with model thickness, enabling STEM-FEM simulations using
models of the same thicknesses as measured experimentally and an
improved ability to relate atomic models and experimental measurements
of glassy materials.
 <
Download (github) >
When a material is bombarded with electrons, a series of scattering processes take place inside it through collisions with ions and other electrons. Through these collisions, electrons already existing in the material receive sufficient energy from the incoming electrons to become activated, leaving their initial positions and initiationg their own internal scattering trajectories. As described in this paper, a fraction of those 'secondary' electrons makes it back to the surface of the material, resulting in a net nonzero emission rate. The package linked here contains Python files to simulate electron scattering processes both in metallic and ceramic materials.
<
Download (github) >
When a material is bombarded with electrons, a series of scattering processes take place inside it through collisions with ions and other electrons. Through these collisions, electrons already existing in the material receive sufficient energy from the incoming electrons to become activated, leaving their initial positions and initiationg their own internal scattering trajectories. As described in this paper, a fraction of those 'secondary' electrons makes it back to the surface of the material, resulting in a net nonzero emission rate. The package linked here contains Python files to simulate electron scattering processes both in metallic and ceramic materials.
 <
Download (github) >
The code package in item 6a above is for flat (ideal) surfaces. However, real material surfaces are never perfectly flat. Moreover, particle irradiation can result over time in significant morpohological changes that create roughness and structure. Hence, methods that can capture surface evolution as surfaces are irradiated are needed for morphology predictions. As described in our paper, raytracing Monte Carlo coupled to surface mesh evolution provides an ideal platform to study irradiation of arbitrary surface geometries, such as the microfoam structure shown in the figure. The package linked here contains a raytracing module that simulates single particle ray interactions with discrete surface elements of a given mesh. These interactions are determined according to the phsyics of electron--matter or ion-matter interactions (as described in 6a), which are characterized using scattering Monte Carlo simulations. Lastly, a mesh evolution module gives the time behavior of the structure if and when appropriate.
<
Download (github) >
The code package in item 6a above is for flat (ideal) surfaces. However, real material surfaces are never perfectly flat. Moreover, particle irradiation can result over time in significant morpohological changes that create roughness and structure. Hence, methods that can capture surface evolution as surfaces are irradiated are needed for morphology predictions. As described in our paper, raytracing Monte Carlo coupled to surface mesh evolution provides an ideal platform to study irradiation of arbitrary surface geometries, such as the microfoam structure shown in the figure. The package linked here contains a raytracing module that simulates single particle ray interactions with discrete surface elements of a given mesh. These interactions are determined according to the phsyics of electron--matter or ion-matter interactions (as described in 6a), which are characterized using scattering Monte Carlo simulations. Lastly, a mesh evolution module gives the time behavior of the structure if and when appropriate.
 <
Download (github) >
SPF (stochastic phase field) is a collection of functions and
executables written to demonstrate stochastically driven field
evolution using a fixed time increment and a rectangular grid, driven
by either continuous-in-time Gaussian noise or discrete Poisson noise
representative of either Brownian motion or a jump process,
respectively. Special care is given to the methods required to
accurately integrate the stochastic differential equations.
Specifically, SPF contains an implementation of the Marcus canonical
integral applicable to Levy processes. SPF is parallelized by MPI and
released under GPLv2. Work done in collaboration with
Prof. Enrique Martinez .
<
Download (github) >
SPF (stochastic phase field) is a collection of functions and
executables written to demonstrate stochastically driven field
evolution using a fixed time increment and a rectangular grid, driven
by either continuous-in-time Gaussian noise or discrete Poisson noise
representative of either Brownian motion or a jump process,
respectively. Special care is given to the methods required to
accurately integrate the stochastic differential equations.
Specifically, SPF contains an implementation of the Marcus canonical
integral applicable to Levy processes. SPF is parallelized by MPI and
released under GPLv2. Work done in collaboration with
Prof. Enrique Martinez .

